Bubble sort, sometimes incorrectly referred to as sinking sort, is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. The algorithm gets its name from the way smaller elements "bubble" to the top of the list. Because it only uses comparisons to operate on elements, it is a comparison sort. Although the algorithm is simple, most of the other sorting algorithms are more efficient for large lists.
Example -- 8 6 7
Compare 8 and 6 and re arrange to 6,8,7
Next number compare 8 and 7 and rearrange 6,7,8
This process continues till there is no swaping
Output : 6,7,8
Quick Sort: Pivot
Compare 8 and 6 and re arrange to 6,8,7
Next number compare 8 and 7 and rearrange 6,7,8
This process continues till there is no swaping
Output : 6,7,8
Average : n^2 and
worst case n lon(n)
Quick Sort: Pivot
Quicksort is a divide and conquer algorithm. Quicksort first divides a large list into two smaller sub-lists: the low
elements and the high elements. Quicksort can then recursively sort the
sub-lists.
The steps are:
1. Pick an
element, called a pivot, from the list.
2. Reorder
the list so that all elements with values less than the pivot come before the
pivot, while all elements with values greater than the pivot come after it
(equal values can go either way). After this partitioning, the pivot is in its
final position. This is called the partition operation.
3. Recursively sort the sub-list of lesser
elements and the sub-list of greater elements.
The base case of the recursion are lists of size
zero or one, which never need to be sorted.
Average: n log n
Worst : n^2
Merge Sort
a merge sort works as follows
1.
Divide
the unsorted list into n sublists, each containing 1 element (a
list of 1 element is considered sorted).
2.
Repeatedly merge sublists to produce new
sublists until there is only 1 sublist remaining. This will be the sorted list.
Example 4 8 9 0
Devide till single element :
4 || 8 || 9 || 0
Group into 2 : 4 8 || 0
9
Merge these 2 list : 0 4 8 9
Avg case : n ( log n )
Worst case: n long (n)
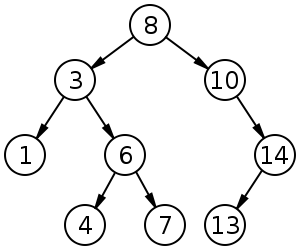
Binary Search tree:
In computer science, a binary
search tree (BST),
which may sometimes also be called an ordered or sorted
binary tree, is a node-based binary tree data structure which has the following properties:
· The left subtree of a node contains only
nodes with keys less than the node's key.
· The right
subtree of a node contains only nodes with keys greater than the node's key.
· Both the
left and right subtrees must also be binary search trees.
· There
must be no duplicate nodes.
Best case : O (1)
Avg case : O (log n )
Avg case : O (log n )
Worst case : O (log n)
SkipList:
A skip list is built in layers. The bottom layer is an ordinary ordered linked list. Each higher layer acts as an "express lane" for the lists below, where an element in layer i appears in layer i+1 with some fixed probability p (two commonly used values for p are 1/2 or 1/4). On average, each element appears in 1/(1-p) lists, and the tallest element (usually a special head element at the front of the skip list) in lists.A search for a target element begins at the head element in the top list, and proceeds horizontally until the current element is greater than or equal to the target.
If the current element is equal to the target, it has been found. If the current element is greater than the target, or the search reaches the end of the linked list, the procedure is repeated after returning to the previous element and dropping down vertically to the next lower list. The expected number of steps in each linked list is at most 1/p, which can be seen by tracing the search path backwards from the target until reaching an element that appears in the next higher list or reaching the beginning of the current list. Therefore, the total expected cost of a search is which is when p is a constant. By choosing different values of p, it is possible to trade search costs against storage costs.
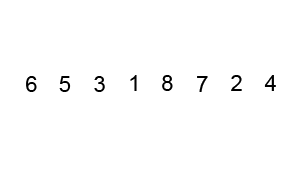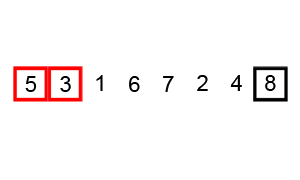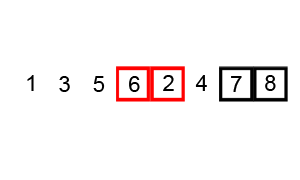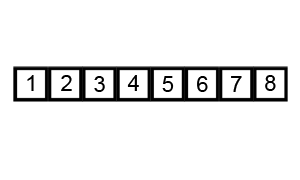



Bubble sort worst case performance is O(n^2) and not O(n logn).
ReplyDeleteThank you for this Information !!
ReplyDeleteLINUX INTERVIEW QUESTIONS
Linux FTP vsftpd Interview Questions
SSH Interview Questions
Apache Interview Questions
Nagios Interview questions
IPTABLES Interview Questions
Ldap Server Interview Questions
LVM Interview questions
Sendmail Server Interview Questions
Read more at Linux Troubleshooting
Hi There,
ReplyDeleteSmokin hot stuff! You’ve trimmed my dim. I feel as bright and fresh as your prolific website and blogs!
I have to print documents using java
I have looking awt.print lib but it is to print text not document. Doc
Follow my new blog if you interested in just tag along me in any social media platforms!
Thank you
Morgan
Very nice post here and thanks for it .I always like and such a super contents of these post.Excellent and very cool idea and great content of different kinds of the valuable information's.
ReplyDeleteangularjs Training in bangalore
angularjs Training in btm
angularjs Training in electronic-city
angularjs Training in online
Data structure questions are crucial for Java developers to assess problem-solving and algorithmic thinking skills. Topics include arrays, linked lists, stacks, queues, hashmaps, trees, and graphs. Developers should understand concepts like time and space complexity, traversal techniques, and data manipulation. Practical coding tasks, such as implementing a binary search tree or optimizing an algorithm, are common. These questions test core programming knowledge, logical reasoning, and the ability to choose appropriate structures for specific problems, ensuring candidates can handle real-world challenges in Java-based applications effectively and efficiently.
ReplyDeleteThank you.
Data science Courses in Berlin